Finite State Machine With Datapath (FSMD)

An FSM (Finite State Machine) is a logical construct which contains a set of states, and a series of directed edges between the states denoting a transition from the origin state to the destination state. Each transition has an associated condition, so that the transition only takes place if the FSM is in a particular state, and the condition is satisfied. In each state, there can be an associated value that's output by the FSM; if the output value is a function of the current state only, then the FSM is a "Moore-type" state machine, else if the output value is a function of both the current state, and the inputs to the FSM, then the FSM is a "Mealy-type" state machine.

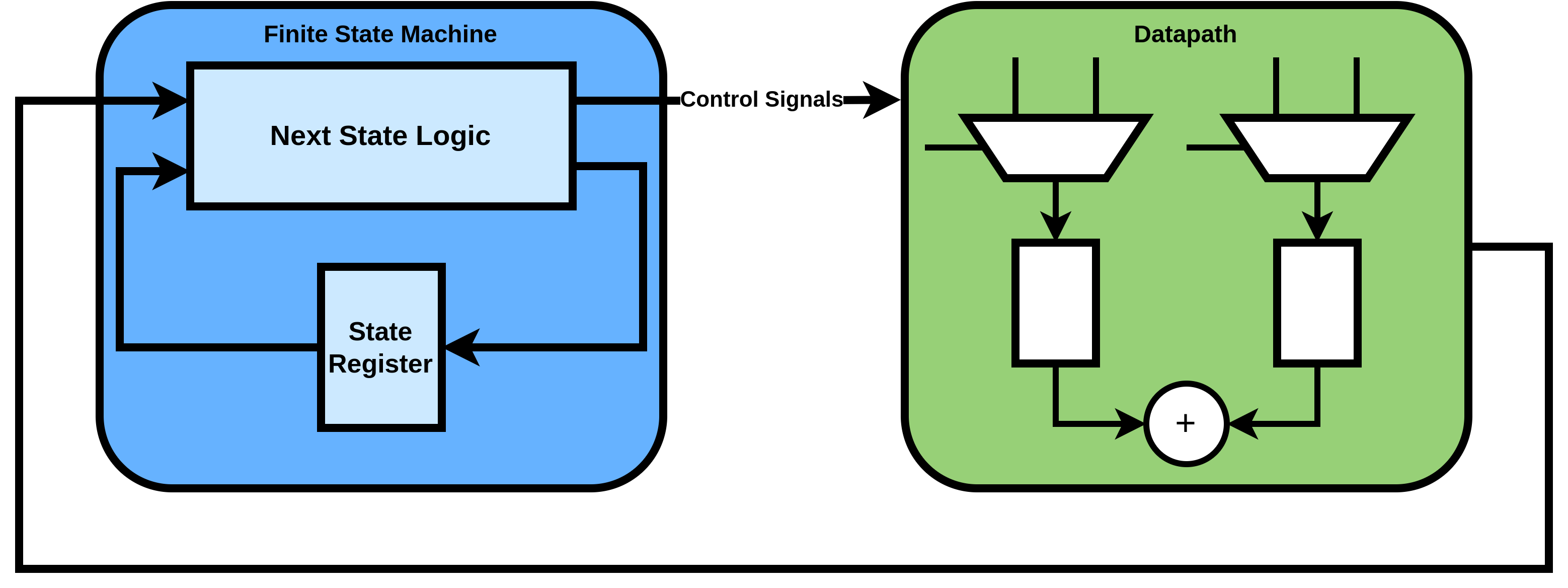
An FSMD (Finite State Machine with Datapath) is an extension to the FSM. An FSM comprises purely the logic explained above; a set of states with some boolean transition conditions. An FSMD includes a "datapath" comprising computational elements (arithmetic units, registers, comparators, etc.) which can accompany a state. In a given state, the FSM provides control signals to indicate what computations the datapath should be undertaking at a given point.

The Greatest Common Divisor Algorithm

One particular GCD algorithm, the Euclidean Algorithm, is a convenient example to consider. The greatest common divisor of two numbers, call them \(a\) and \(b\), is simply the largest number, call it \(c\), which is a divisor of both \(a\) and \(b\). That is, if \(\mathrm{gcd}(a,b) = c\), then \(cd = a\) and \(ce = b\), and \(c\) is the largest possible integer which satisfies these expressions. Euclid's Algorithm is able to compute the GCD of two numbers by taking advantage of the fact that the common divisors of \(a\) and \(b\) are the same as \(a - b\) and \(b\) (this is obviously true since if \(c\) is a divisor of \(a\) and \(b\), then \(a - b = a - ce\), and since \(e\) is an integer, then \(\frac{a - ce}{c} = \frac{a}{c} - e\)).

We can reformulate the above using modular arithmetic to arrive at the Euclidean Algorithm; assuming \(a > b\), then \(a = qb + r\) where \(r\) is a remainder and \(q\) is some integer. Since \(c\) is a divisor of \(a\), \(b\) and \(qb\), then it must also be a divisor of \(r = qb - a\), and as a result \(\mathrm{gcd}(a,b) = \mathrm{gcd}(b,r)\). Using this, we can implement the Euclidean Algorithm as follows:

int gcd(int a, int b) {
    if (a < b) {
        std::swap(a, b);
    }

    while (b != 0) {
        int r = a % b;
        a = b;
        b = r;
    }

    return a;
}

Let's see what this looks like in LLVM IR:

define i32 @gcd(i32 %a, i32 %b) {
; If (a < b), branch to swap, else continue
entry:
    %cmp = icmp slt i32 %a, %b
    br i1 %cmp, label %if.then, label %if.end

; a < b, branch to swap (lets us use phi)
if.then:
    br label %if.end

; If a < b, then swap, else use input values, then begin looping
if.end:
    %a.addr = phi i32 [ %b, %if.then ], [ %a, %entry ]
    %b.addr = phi i32 [ %a, %if.then ], [ %b, %entry ]
    br label %while.cond

; If loop start, then take (potentially swapped) inputs, otherwise, a <= b 
; and b <= r from loop update. Then check whether b == 0 and branch
; accordingly
while.cond:
    %b.addr1 = phi i32 [ %b.addr, %if.end ], [ %r, %while.body ]
    %a.addr2 = phi i32 [ %a.addr, %if.end ], [ %b.addr1, %while.body ]
    %cmp1 = icmp ne i32 %b.addr1, 0
    br i1 %cmp1, label %while.body, label %while.end

; Update step where a <= b and r <= (a % b), then branch back to check
while.body:
    %rem = srem i32 %a.addr2, %b.addr1
    %r = add i32 %rem, 0
    br label %while.cond

; Output result
while.end:
    ret i32 %a.addr2
}

The basic blocks provide a convenient starting point to construct our FSMD states. We see that it doesn't quite provide the optimal FSMD; for instance, we don't need the if.then basic block since this is purely there to accommodate the phi instruction in if.end. Rather, we could branch directly to if.end from entry, but for the moment we're not too interested in optimising. Let's draw this out explicitly and consider an example where we're trying to find the \(\mathrm{gcd}(6, 12)\).

Implementation

Translating the IR from the previous section into VHDL is straightforward. First of all, we define the interface to the FSMD:

entity gcd is
  port(
    clk   : in  std_logic;
    rst   : in  std_logic;
    start : in  std_logic;
    a     : in  unsigned(31 downto 0);
    b     : in  unsigned(31 downto 0);
    done  : out std_logic;
    gcd   : out unsigned(31 downto 0)
    );
end gcd;

There are a number of ways to write an FSMD using VHDL; different practitioners will split an FSM into a number of different processes. The style we choose is to have a clocked process which drives the registering of data and the current state:

  state_logic : process(clk) is
  begin
    if rising_edge(clk) then
      if rst = '1' then
        state <= ENTRY;
        a_reg <= (others => '0');
        b_reg <= (others => '0');
        gcd   <= (others => '0');
        done  <= '0';
      else
        state <= next_state;
        a_reg <= a_next;
        b_reg <= b_next;

        if state = WHILE_END then
          gcd  <= a_reg;
          done <= '1';
        else
          done <= '0';
        end if;
      end if;
    end if;
  end process state_logic;

along with a combinational process containing the logic for driving the next state and computing intermediary results.

  next_state_logic : process(all) is
  begin
    next_state <= state;
    a_next     <= a_reg;
    b_next     <= b_reg;
    swapped_a  <= b_reg;
    swapped_b  <= a_reg;

    case state is
      when ENTRY =>
        if start = '1' then
          a_next <= a;
          b_next <= b;

          if a < b then
            next_state <= IF_THEN;
          else
            next_state <= IF_END;
          end if;
        end if;

      when IF_THEN =>
        a_next     <= swapped_a;
        b_next     <= swapped_b;
        next_state <= IF_END;

      when IF_END =>
        next_state <= WHILE_COND;

      when WHILE_COND =>
        if b_reg = 0 then
          next_state <= WHILE_END;
        else
          next_state <= WHILE_BODY;
        end if;

      when WHILE_BODY =>
        a_next     <= b_reg;
        b_next     <= a_reg rem b_reg;
        next_state <= WHILE_COND;

      when WHILE_END =>
        next_state <= WHILE_END;
    end case;
  end process next_state_logic;

This is perhaps a little disconnected from what the FSMD is meant to represent; recall that an FSMD is an FSM which creates control signals to drive an algorithmic datapath. Yet in our implementation, the datapath appears to accompany the state transition logic, so the two appear to be merged somewhat. While the conceptual picture of an FSMD can clearly be realised as an actual design, it's principally a model that's convenient to think of. Ultimately, the synthesis tools are free to implement whatever it deems most efficient; so long as the result transitions between the set of states we specify and yields the correct result, whether or not the actual RTL directly mirrors the FSMD is irrelevant.

An Aside: Structure

There may be certain situations where it's perhaps beneficial to retain the separation between FSM and datapath. The following example is taken from FPGA Prototyping by Verilog Examples:

case state is
begin
    when S1 =>
        x <= reg_a * reg_b;
    when S2 =>
        y <= reg_c * reg_d;
    when S3 =>
        z <= reg_e * reg_f;
    ...
end case;

The synthesiser may decide to implement this using three separate multipliers, but since only a single state can be scheduled at a time, only a single resource is required. We could help the synthesiser:

case state is
begin
    when S1 =>
        mult_a <= reg_a;
        mult_b <= reg_b;
        x <= mult_result;
    when S2 =>
        mult_a <= reg_c;
        mult_b <= reg_d;
        y <= mult_result;
    when S3 =>
        mult_a <= reg_e;
        mult_b <= reg_f;
        z <= mult_result;
    ...
end case;

mult_result <= mult_a * mult_b;

Now the result of the multiplication happens in a combinational path that's separate from the FSM logic, and it's clear that a single multiplier resource should be used. Undoubtedly modern synthesisers are probably able to work this out for themselves, but this structure also makes it clear to the reader that the intention is to use a single multiplier resource.