Basic Scheduling
Posted on Sun 17 November 2024 in high_level_synthesis
The objective of this section is to explain how one might take a CFG and generate a schedule. Generally speaking, a schedule is a mapping from each operation in the CFG to the earliest time at which it is feasible for that operation to be executed. More concretely, for the operation at vertex \(v_k\), if the earliest time at which \(v_k\) can be scheduled is \(t(v_k)\), then
and requires the initial constraint
This is referred to as the as soon as possible (ASAP) schedule, since an operation is scheduled as soon as it's possible to do so.
There are a number of different scheduling algorithms one might adopt; the complement to the ASAP schedule is the as late as possible (ALAP) schedule. Here, a maximum time at which all operations must be completed by, \(T\), is provided, and the scheduling function takes the form
with the initial constraint
Clearly if \(T\) is chosen too small, then we could end up with negative \(t(v_k)\). With the ALAP schedule, operations are scheduled at the latest possible increment so that successor timing can be met. We'll come to a comparison between ASAP and ALAP schedules in a later post, but suffice to say neither is necessarily better, they're just different heuristics for computing a feasible schedule.
Topological Sorting
A topologically sorted graph is an ordered list of vertices, where each vertex is listed after all of its direct predecessors. For a simple linear graph, say \(A \rightarrow B \rightarrow C\), the topological ordering is simple; it's just \([A,B,C]\). It's useful at this point to introduce the concept of domination; a vertex \(v\) is said to dominate another vertex \(u\) if all paths from the entry node to \(u\) go through \(v\). Since \(B\) is dominated by \(A\), \(B\) succeeds \(A\) in the topological sort. Similarly, since \(C\) is dominated by \(B\) and transitively by \(A\), it succeeds both of them.
How about something a little more complex, say the diamond graph comprising four vertices, \(\{A,B,C,D\}\), with the edges \((A,B),(A,C),(B,D),(C,D)\). Since \(A\) dominates all paths, clearly it must be the first element of the topological sort. Furthermore, since \(D\) is the final node in the graph, it must be the final element of the topological sort. However, there's no clearly an ambiguity; neither \(B\) nor \(C\) are dominated by each other -- they're both at the same level of the graph. The topological sort isn't a unique ordering, and hence both \([A,B,C,D]\) and \([A,C,B,D]\) are valid topological sorts of the graph.
For the sake of practice, consider a final graph:
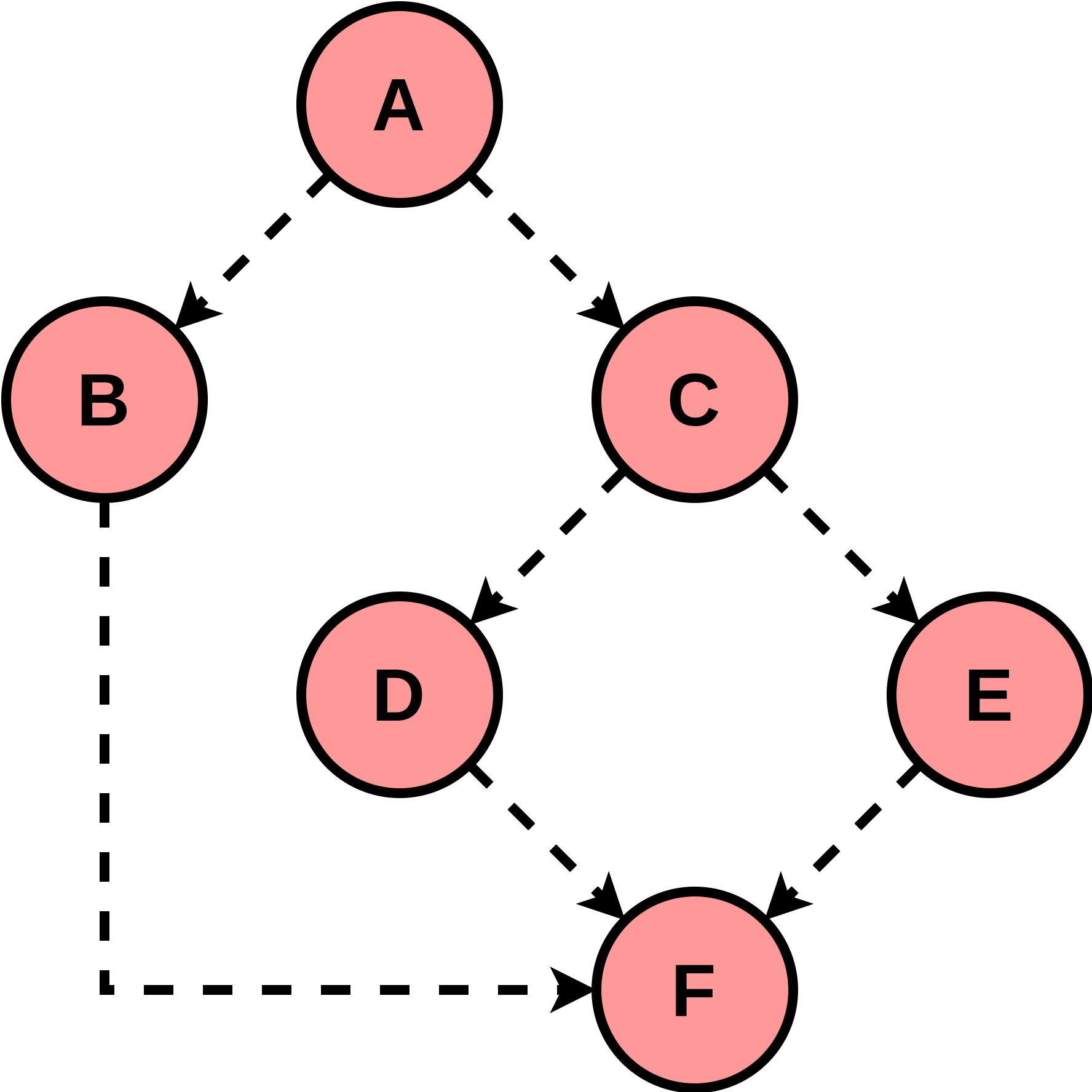
Again, it's clear that the first and final elements of the topological sort are \(A\) and \(F\), respectively. \(B\) and \(C\) are not connected (or rather, there is no edge set which forms a path between \(B\) and \(C\)), hence an ambiguity in their ordering. Similarly \(D\) and \(E\) are not connected, resulting in another ambiguity. However, neither \(D\) nor \(E\) are connected to \(B\), so there's a final ambuguity. Consequently, there are several valid topological sorts:
| Sort 1 | \(\left[ A, B, C, D, E, F\right]\) |
| Sort 2 | \(\left[ A, B, C, E, D, F\right]\) |
| Sort 3 | \(\left[ A, C, B, D, E, F\right]\) |
| Sort 4 | \(\left[ A, C, B, E, D, F\right]\) |
| Sort 5 | \(\left[ A, C, B, D, E, F\right]\) |
| Sort 6 | \(\left[ A, C, B, E, D, F\right]\) |
Depth-First Search
The strategy we discuss here to generate the topologically-sorted graph uses the depth-first search. This algorithm is covered in nauseating detail in millions of blog posts, and consequently its mechanics shan't be discussed here. Rather, let's work an example of the depth-first search on the graph provided in the previous section, and convince ourselves that it traverses the graph in topological order. More specifically, we'll use the post-order depth-first search, where a node is only added to the list after all of its predecessors have been added.
Clearly the result here is the reverse of a topological sort; the vertex with no successors is the first element of the sorted list. The topological sort can be recovered through explicitly reversing the list, or simply traversing it in reverse order when required.
Generating A Schedule
Now that we have a topological sort of our graph, we're able to generate a feasible schedule. Let's consider an implementation of the ASAP schedule:
std::map<Node, int> schedule;
for (const auto& node : nodes) {
int latest = -1;
for (const auto& predecessor : predecessors(node)) {
latest = std::max(latest, schedule[node]);
}
schedule[node] = latest + 1;
}
And that's it! If we apply this to the graph of the previous section, we'd find the following schedule:
| Time Increment | Vertices Scheduled |
|---|---|
| 0 | \(A\) |
| 1 | \(B, C\) |
| 2 | \(E, D\) |
| 3 | \(F\) |
Which is precisely what we expect; \(B\) and \(C\) can be evaluated concurrently, as can \(D\) and \(E\). The entire graph can be computed with a latency of 3.
An Example: The Adder Tree
Let's try to apply the above to a concrete example. The simplest non-trivial one which is at least somewhat interesting that I like to think of is the function \(f(x,n) = 2^nx\). The reason is that this function can be implemented as a simple \(n\)-stage adder tree, where a single input value \(x\) is distributed to each input node of the tree. Let's take an explicit example, with \(n = 2\) and \(x = 4\), which should yield the result \(4\times 2^2 = 16\). Drawing this out:
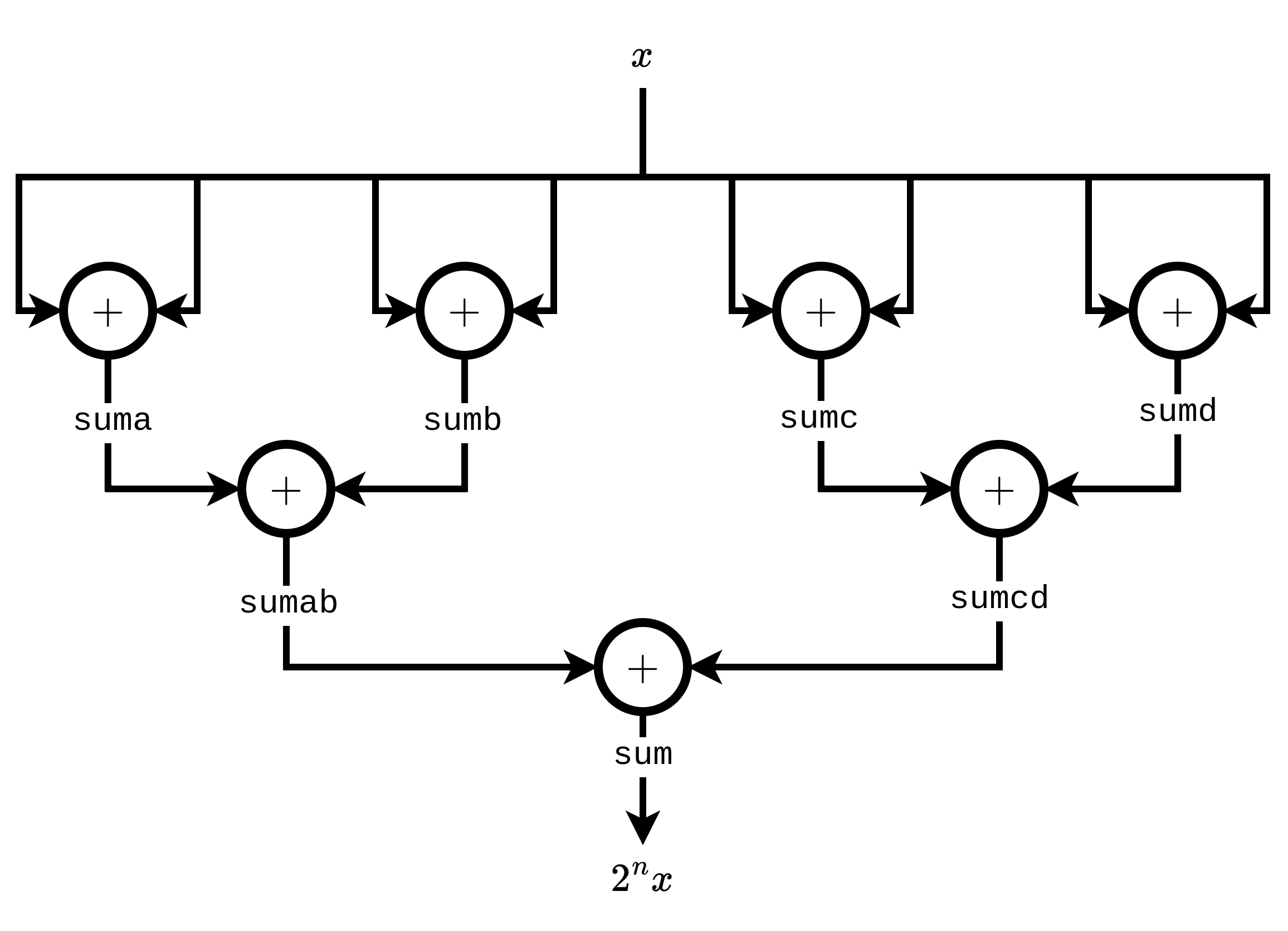
Conveniently, this maps directly to a DFG whose LLVM IR can be written as:
define i32 @three_stage_adder(i32 %x) {
entry:
%suma = add i32 %x, %x
%sumb = add i32 %x, %x
%sumc = add i32 %x, %x
%sumd = add i32 %x, %x
%sumab = add i32 %suma, %sumb
%sumcd = add i32 %sumc, %sumd
%sum = add i32 %sumab, %sumcd
ret i32 %sum
}
Manually applying the algorithm explained above to derive a schedule from topologially-sorted list of nodes, sum_d is considered first; since it has no predecessors, it can be scheduled at time \(t = 0\). The same logic holds for sum_c, which can be scheduled concurrently with sum_d. We encounter sum_cd next, whose predecessors have both been scheduled at \(t = 0\), and consequently sum_cd can be scheduled at \(t = 1\). Next we consider sum_b and sum_a, both of which have no predecessors and are free to be scheduled at \(t = 0\). sum_ab is consequently scheduled at \(t = 1\), and finally we arrive at sum, whose predecessors sum_ab and sum_cd have been scheduled at \(t = 1\), freeing us to schedule sum at \(t = 2\). So the time at which a node can be scheduled corresponds to the level of the adder tree which the node sits in. As a result, we've extracted the maximum amount of parallelism from our DFG, and the schedule is considered, at least from a performance perspective, optimal.
| Time Increment | Operations Scheduled |
|---|---|
| 0 | suma, sumb, sumc, sumd |
| 1 | sumab, sumcd |
| 2 | sum |